Week 3: Sampling distributions

Wed, Feb 14, 2018 Made by Judit Kisistók, incorporating some snippets from Moisés Coll Maciá's solution sheet. The R exercise session was created by Thomas Bataillon and Palle Villesen at Aarhus University.

Table of contents
Loading libraries
Problem 9
Exercises

Loading libraries

library(abd) #we need to load the ABD dataset to be able to access the YeastGenes data in Exercise 1
library(cowplot) #this is just for plotting but you don't need to worry about it

Chapter 4, Problem 9

One of the great discoveries of biology is that organisms have a class of genes called “regulatory genes”, whose only job is to regulate the activity of other genes. How many genes does the typical regulatory gene regulate? A study of interaction networks in yeast (S. cerevisiae) came up with the following data for 109 regulatory genes (Guelzim et al. 2002).

Loading the data and taking a peek at the summary:

regulatedGenes=read.csv("chap04q09NumberGenesRegulated.csv") 
#read.csv() function - use this whenever you have comma-separated data (aka a csv)
summary(regulatedGenes)

##      ngenes      
##  Min.   : 1.000  
##  1st Qu.: 2.000  
##  Median : 6.000  
##  Mean   : 8.312  
##  3rd Qu.:12.000  
##  Max.   :37.000

What type of graph should be used to display these data?

A histogram:

hist(regulatedGenes$ngenes, breaks=30, col="cornflowerblue",
     xlab="Number of genes regulated", main="Regulatory genes in yeast")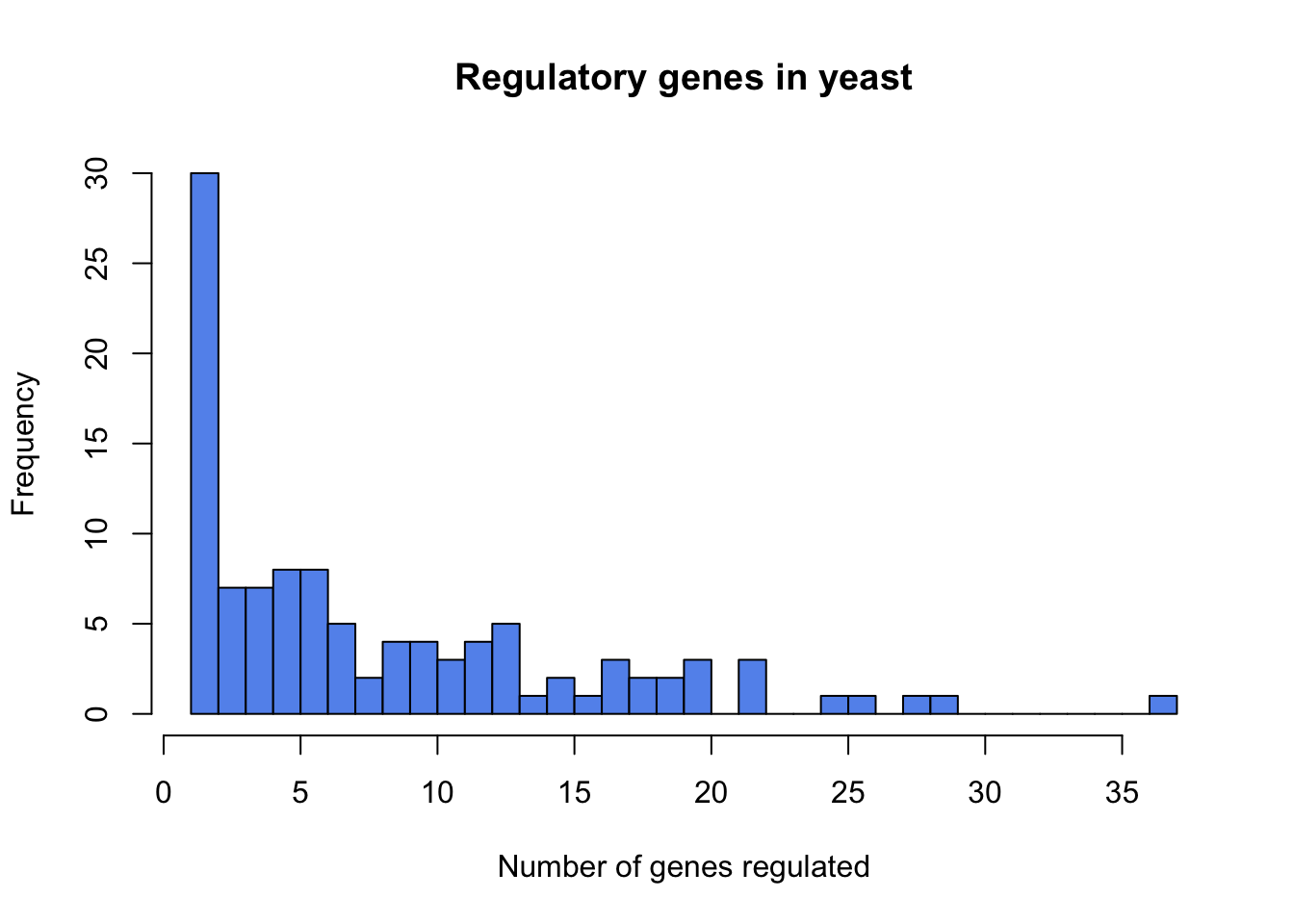

What is the estimated mean number of genes regulated by a regulatory gene in the yeast genome?

mean(regulatedGenes$ngenes)

## [1] 8.311927

median(regulatedGenes$ngenes) #just for reference

## [1] 6

What is the standard error of the mean?

sd(regulatedGenes$ngenes)/sqrt(109)

## [1] 0.7233423

# the standard error is the standard deviation divided by the square root of the sample size and here the sample size is 109

Explain what this standard error measures and what assumptions are we making when calculating it.

We assume that:

the sample is obtained through random sampling
the statistic is distributed symmetrically

Take me back to the beginning!

Exercises

1. Reproducing the Figure 4.1-1 & important details of histogram drawing in R

data(HumanGeneLengths) # loading the data of example 4.1 of the book

Take a quick peek at the data and try to find the size of the titin gene (hint: footnote on page 97)

summary(HumanGeneLengths)

##   gene.length   
##  Min.   :   60  
##  1st Qu.: 1312  
##  Median : 2226  
##  Mean   : 2622  
##  3rd Qu.: 3444  
##  Max.   :99631

Since we know that the longest human gene is the one encoding titin, we can find its length by looking at the Max value in the summary - 99631 nt.

How many genes are in the dataset?

dim(HumanGeneLengths)

## [1] 20290     1

# this indicates the number of rows and the number of columns in the data - hence, the number of genes (20290) and the number of variables (1 - gene length)

Draw a histogram:

hist(HumanGeneLengths$gene.length, breaks=50, col="deeppink4", main="", xlab="Gene length (nt)")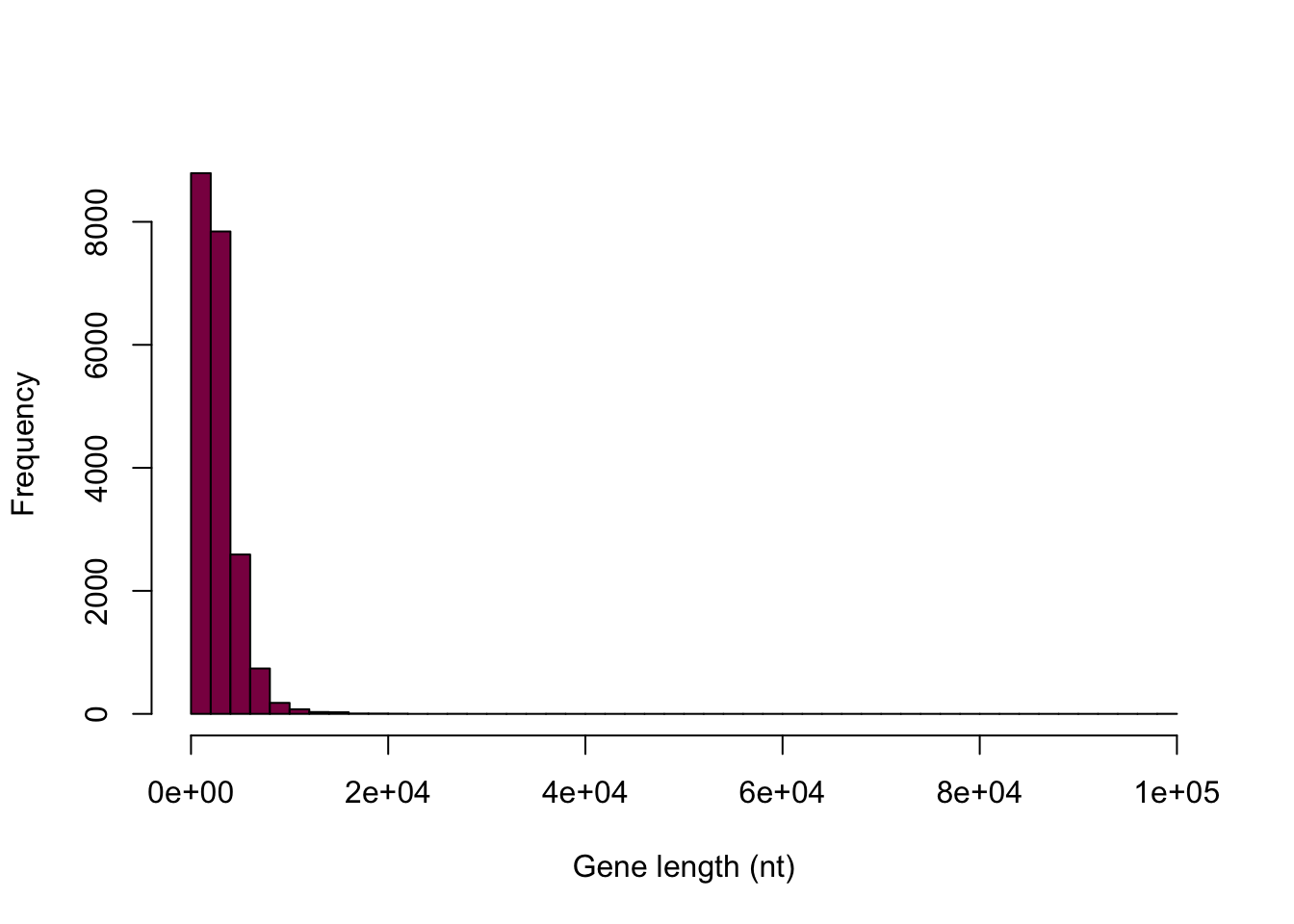

Identify what the options col, main and xlab are allowing you to do.

col: you can add color to your histogram (here is a cool color reference guide if you really want to make it fancy)
main: adds the title to the histogram
xlab: adds the label on the x axis

Why is this graph a BAD display of the data?

Because even though the majority of the data span from 1 to 15000, the histogram above displays the full range up to 10000 - so we get a large empty-looking area. In this case it’s a great idea to say that we want to see a histogram that displays the values between 0 and 15000 - and make a mental note of the “unusual” data point that we disregard in this way.

Are there 50 bins on the following graph? If not, why not?

# we can save the histogram in a variable so that we can gain some information about it later
histdata <- hist(HumanGeneLengths$gene.length, breaks=50, col="deeppink4", main="", xlab="Gene length (nt)",xlim = c(0,15000))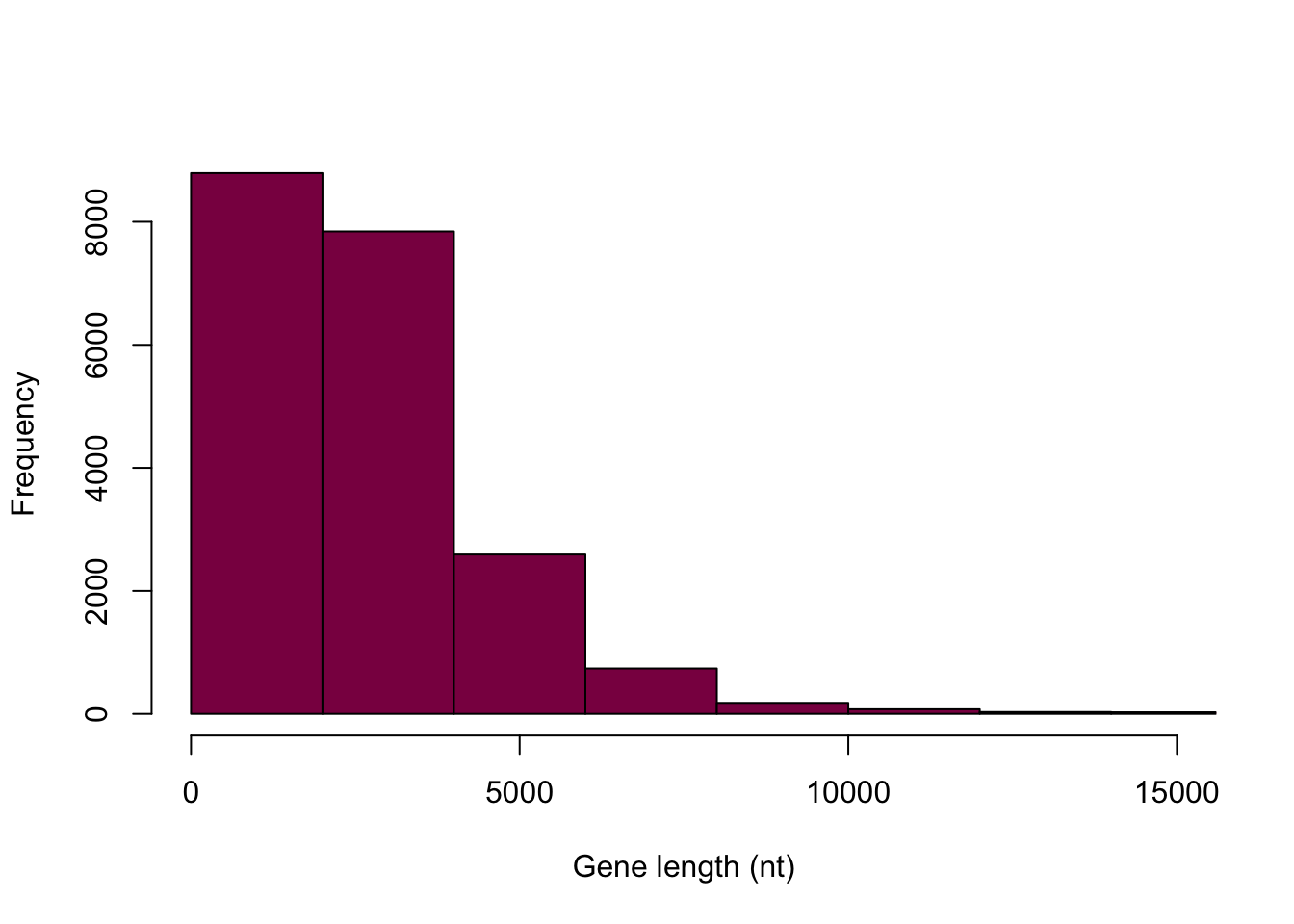

histdata

## $breaks
##  [1]      0   2000   4000   6000   8000  10000  12000  14000  16000  18000
## [11]  20000  22000  24000  26000  28000  30000  32000  34000  36000  38000
## [21]  40000  42000  44000  46000  48000  50000  52000  54000  56000  58000
## [31]  60000  62000  64000  66000  68000  70000  72000  74000  76000  78000
## [41]  80000  82000  84000  86000  88000  90000  92000  94000  96000  98000
## [51] 100000
## 
## $counts
##  [1] 8791 7843 2591  738  179   75   30   26    6    5    3    0    0    1
## [15]    0    0    0    0    1    0    0    0    0    0    0    0    0    0
## [29]    0    0    0    0    0    0    0    0    0    0    0    0    0    0
## [43]    0    0    0    0    0    0    0    1
## 
## $density
##  [1] 2.166338e-04 1.932725e-04 6.384919e-05 1.818630e-05 4.411040e-06
##  [6] 1.848201e-06 7.392804e-07 6.407097e-07 1.478561e-07 1.232134e-07
## [11] 7.392804e-08 0.000000e+00 0.000000e+00 2.464268e-08 0.000000e+00
## [16] 0.000000e+00 0.000000e+00 0.000000e+00 2.464268e-08 0.000000e+00
## [21] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## [26] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## [31] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## [36] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## [41] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## [46] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 2.464268e-08
## 
## $mids
##  [1]  1000  3000  5000  7000  9000 11000 13000 15000 17000 19000 21000
## [12] 23000 25000 27000 29000 31000 33000 35000 37000 39000 41000 43000
## [23] 45000 47000 49000 51000 53000 55000 57000 59000 61000 63000 65000
## [34] 67000 69000 71000 73000 75000 77000 79000 81000 83000 85000 87000
## [45] 89000 91000 93000 95000 97000 99000
## 
## $xname
## [1] "HumanGeneLengths$gene.length"
## 
## $equidist
## [1] TRUE
## 
## attr(,"class")
## [1] "histogram"

# this way we can see the bins, the counts in each bin, etc.

By examining this, we can see that R indeed gave us 50 bins, but it did so over the span of the entire range - we just can’t see most of them because we chose to display our data up to 15000.

Let’s make a vector of breakpoints for the histogram to enforce the same bins as in the book (500 nt). How many breaks are there?

myBreaks=seq(from=0, to=15000,  by=500)
length(myBreaks) #number of breaks

## [1] 31

myBreaks

##  [1]     0   500  1000  1500  2000  2500  3000  3500  4000  4500  5000
## [12]  5500  6000  6500  7000  7500  8000  8500  9000  9500 10000 10500
## [23] 11000 11500 12000 12500 13000 13500 14000 14500 15000

Why does R choke here?

#hist(HumanGeneLengths$gene.length, breaks=myBreaks, xlim = c(0,15000))

It says “some ‘x’ not counted; maybe ‘breaks’ do not span range of ‘x’”.

It’s because we’re essentially creating the breaks up to 15000, however, the biggest data point (the gene encoding titin) has the value 99700.

What are we doing here?

myBreaks=c(seq(from=0, to=15000, by=500),99700) 
myBreaks

##  [1]     0   500  1000  1500  2000  2500  3000  3500  4000  4500  5000
## [12]  5500  6000  6500  7000  7500  8000  8500  9000  9500 10000 10500
## [23] 11000 11500 12000 12500 13000 13500 14000 14500 15000 99700

We are correcting the previous mistake by adding another break between 15000 and 97500, so that the breaks span the entire range of x.

This one is still bad (but at least more fine-grained):

hist(HumanGeneLengths$gene.length, breaks=myBreaks, col = "deeppink4", main = "", xlab="Gene length (nt)")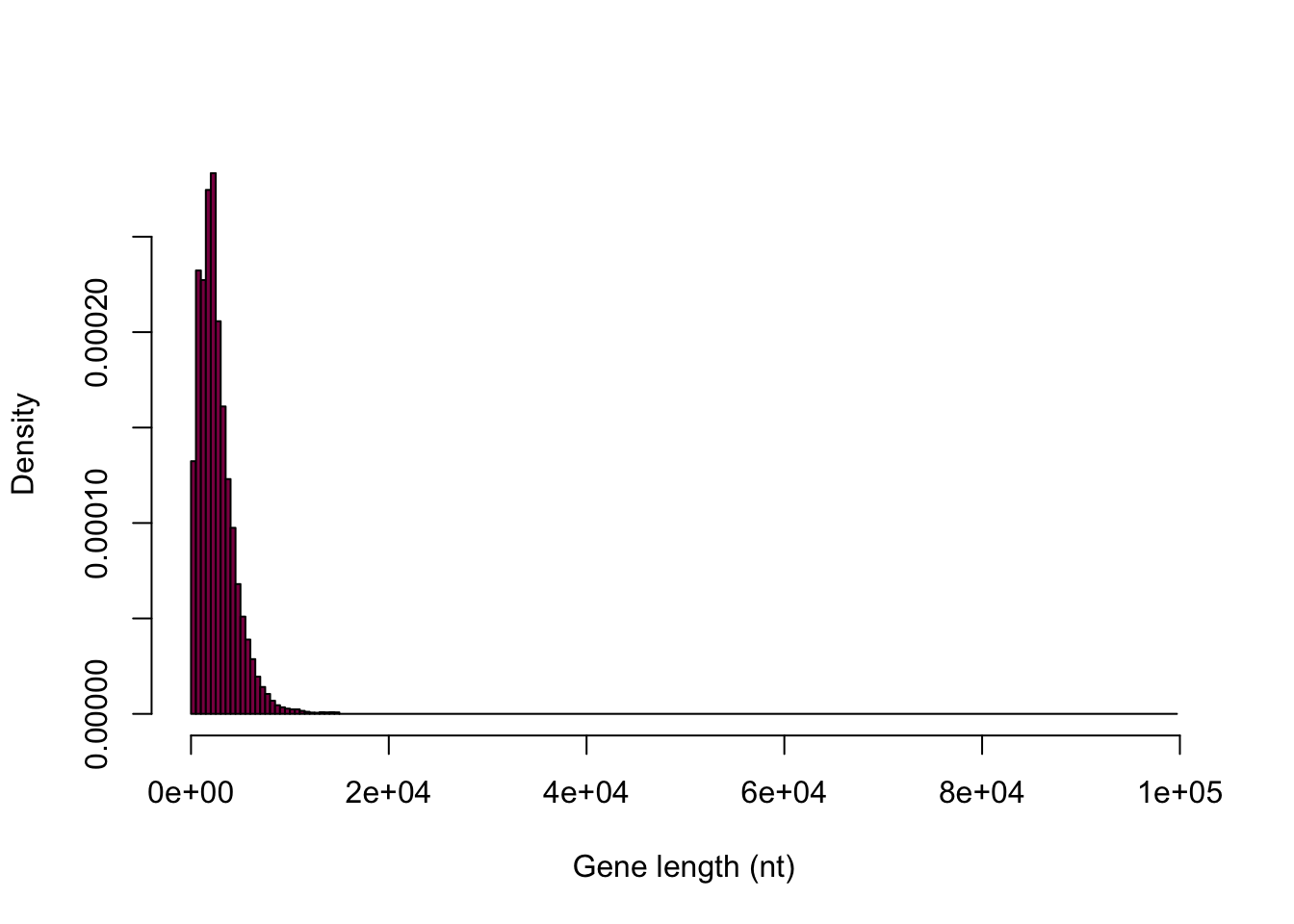

Look at the Y axis: is this the same Y axis as the book?

hist(HumanGeneLengths$gene.length, breaks=myBreaks, xlim = c(0,15000), col="deeppink4", main="", xlab="Gene length (nt)", freq=T)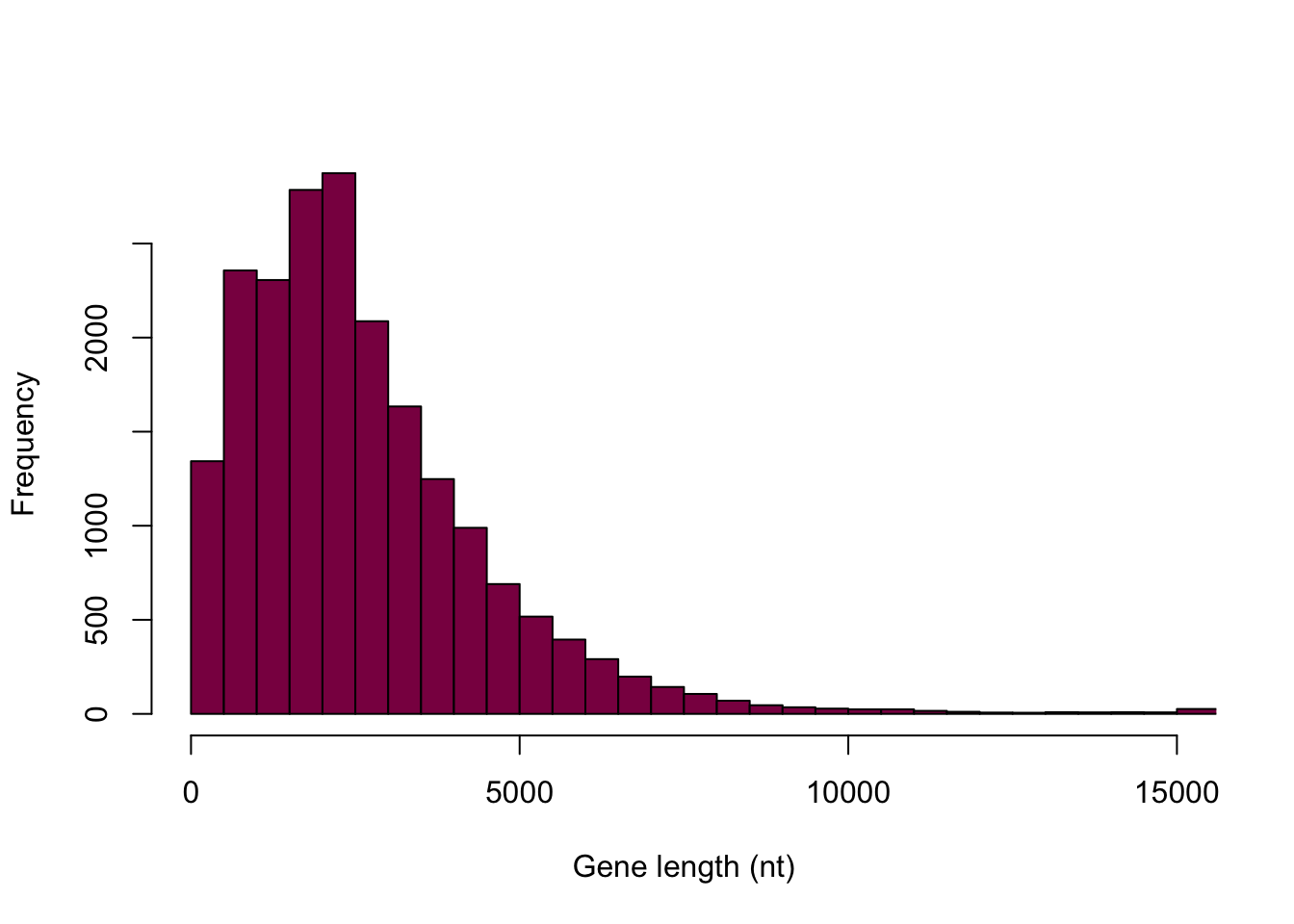

It’s not the same Y axis.

What is the difference between frequency of a class and counts of observation per class?

hist(HumanGeneLengths$gene.length, breaks=myBreaks, xlim = c(0,15000), col="deeppink4", main="", xlab="Gene length (nt)", freq=F)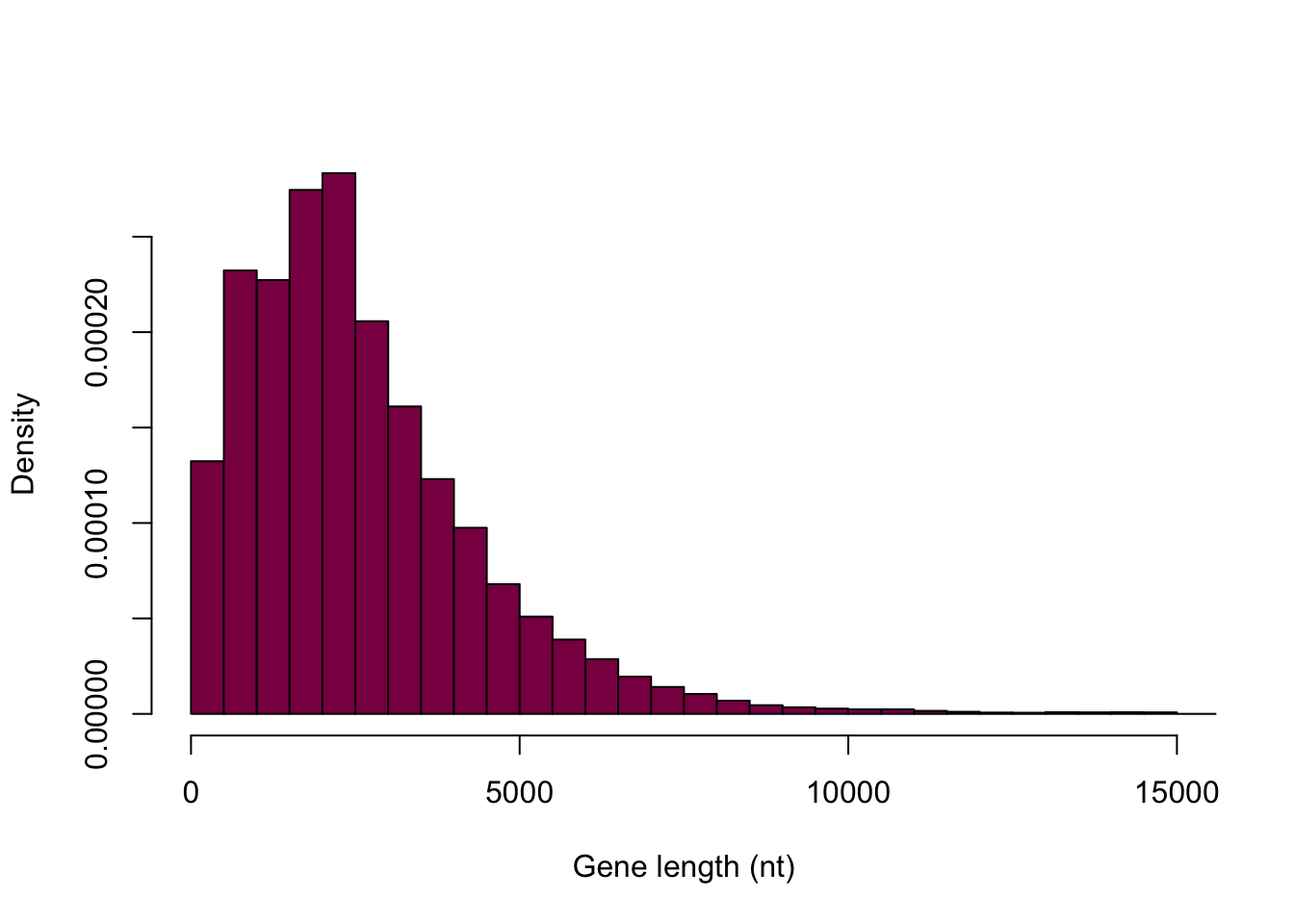

The first histogram displays counts in the bins and adding them together should sum to the number of observations in total. It shows the absolute frequencies. The second histogram displays the relative frequencies (absolute frequency / total number of observations) and should sum up to 1 - this is still not the exact same scale as we see in the book, however, the goal is not to make an exact carbon copy. This is the best we can do here and the point is really just to understand the difference between absolute and relative frequencies.

Take me back to the beginning!

2. Generating Figure 4.1-2

Use the R function sample() to get a vector of 100 observations drawn from HumanGeneLengths and reproduce fig 4.1-2

Hint: Here is a simple example to draw 5 numbers with replacement from a “made-up” empirical distribution - adapt that for your purposes.

madeup=c(3,3,4,5,6,7,8,2,1,3,5,6,12,435,23)
sample(x = madeup, size = 5,replace = T) # Q:what are the options x=, size= and replace=  specifying here (check the help)?

## [1]   3   5   5   4 435

x: the data that we want to draw samples from
size: the size of the sample that we want to take
replace: whether or not we want to sample with replacement

Discuss what is the conceptual difference between replace = T and replace = F (what should we use here?)

replace = T: sampling WITH replacement - when we sample with replacement, the sample values (sampled units) are independent
replace = F: sampling WITHOUT replacement - in this case the sample values are not independent, because what we pick as a first value will affect what we can pick as a second value - this complicates computations

As we want a random sample (where each unit has equal chance of being picked and the selection of units is independent), we should sample with replacement.

hist(sample(x = HumanGeneLengths$gene.length, size = 100,replace = T), 
     breaks=myBreaks, 
     xlim = c(0,15000), 
     col="deeppink4", 
     main="", 
     xlab="Gene length (number of nucleotides)", 
     freq=T)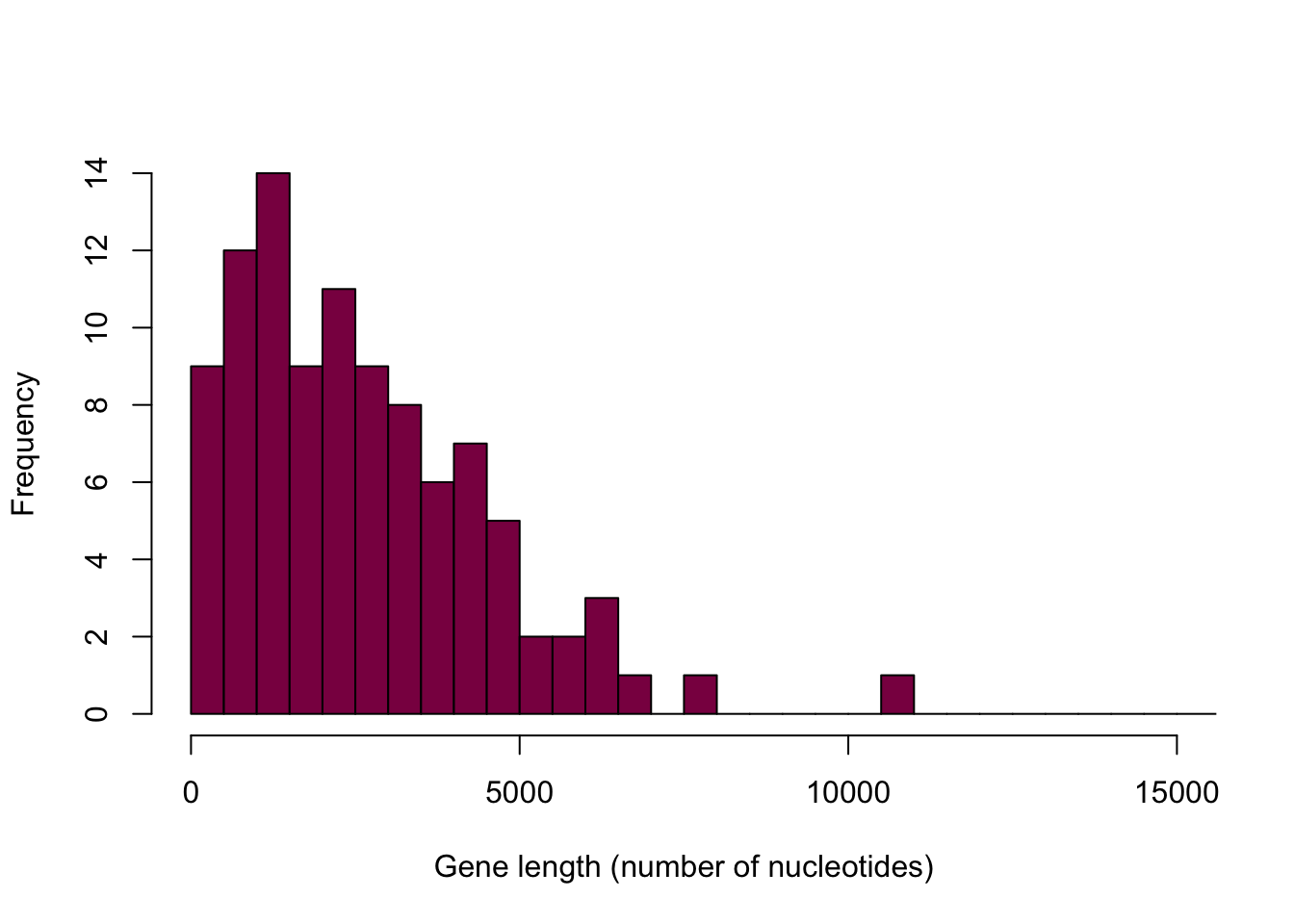

Notice how this histogram is different every single time we run the code - it is due to the randomness in sampling.

Take me back to the beginning!

3. Reproducing Figures 4.1-3 and 4.1-4

Conceptually, to generate by simulation the sampling distribution of mean gene length, we resample 100 datapoints, we calculate the mean in the sample and “write it down” and repeat that operation many times (say 10^4 times).

In most programming languages there is a way to “repeat” a sequence of things x times —> the for loop. Here is one basic example:

for (year in c(2010,2011,2012,2013,2014,2015)){
  print(paste("The year is", year))
}

## [1] "The year is 2010"
## [1] "The year is 2011"
## [1] "The year is 2012"
## [1] "The year is 2013"
## [1] "The year is 2014"
## [1] "The year is 2015"

Here the print statement is executed with various values of the year, but you can also use that to do something just 10 times.

for (i in 1:10) {
  tryit=sample(x = madeup, size = 5,replace = T) #we take the sample
  mymedian=median(tryit) #we calculate the median of the sample
  cat("And the median is: ", mymedian, "\n") #we concatenate and print it out
}

## And the median is:  5 
## And the median is:  5 
## And the median is:  8 
## And the median is:  5 
## And the median is:  4 
## And the median is:  6 
## And the median is:  3 
## And the median is:  6 
## And the median is:  3 
## And the median is:  4

Or we can be smart and instead of “printing it” we “write it down” i.e. store that in a vector:

myMedians = NULL # this initializes a "nullvector"
for (i in 1:10) {
  tryit=sample(x = madeup, size = 5,replace = T)
  myMedians[i]=median(tryit) #we add the calculated medians to the nullvector
}
myMedians

##  [1]  6 23  6 23  4  7  3  7  3  7

Adapt this code to generate fig 4.1-3 and 4.1-4 (use 10^4 samples to get the sampling distributions).

#nullvectors for the means (different sample sizes)
meanLength_100 = NULL
meanLength_20 = NULL
meanLength_500 = NULL

for (i in 1:10000) {
  # taking the samples with different sample sizes
  sample_100 = sample(x = HumanGeneLengths$gene.length, size = 100, replace = T) 
  sample_20 = sample(x = HumanGeneLengths$gene.length, size = 20, replace = T)
  sample_500 = sample(x = HumanGeneLengths$gene.length, size = 500, replace = T)
  # calculating the means
  meanLength_100[i] = mean(sample_100)
  meanLength_20[i] = mean(sample_20)
  meanLength_500[i] = mean(sample_500)
}

par(mfrow=c(3,1)) # creating the 3*1 figure layout

hist(meanLength_20,
     breaks = 80,
     col = "deeppink4",
     main = "Sample size = 20",
     xlab = "", 
     freq = F, 
     xlim = c(1000,5200))

hist(meanLength_100,
     breaks = 80,
     col = "deeppink4",
     main = "Sample size = 100",
     xlab = "", 
     freq = F, 
     xlim = c(1000,5200))

hist(meanLength_500,
     breaks = 80,
     col = "deeppink4",
     main = "Sample size = 500",
     xlab = "Sample mean length", 
     freq = F, 
     xlim = c(1000,5200))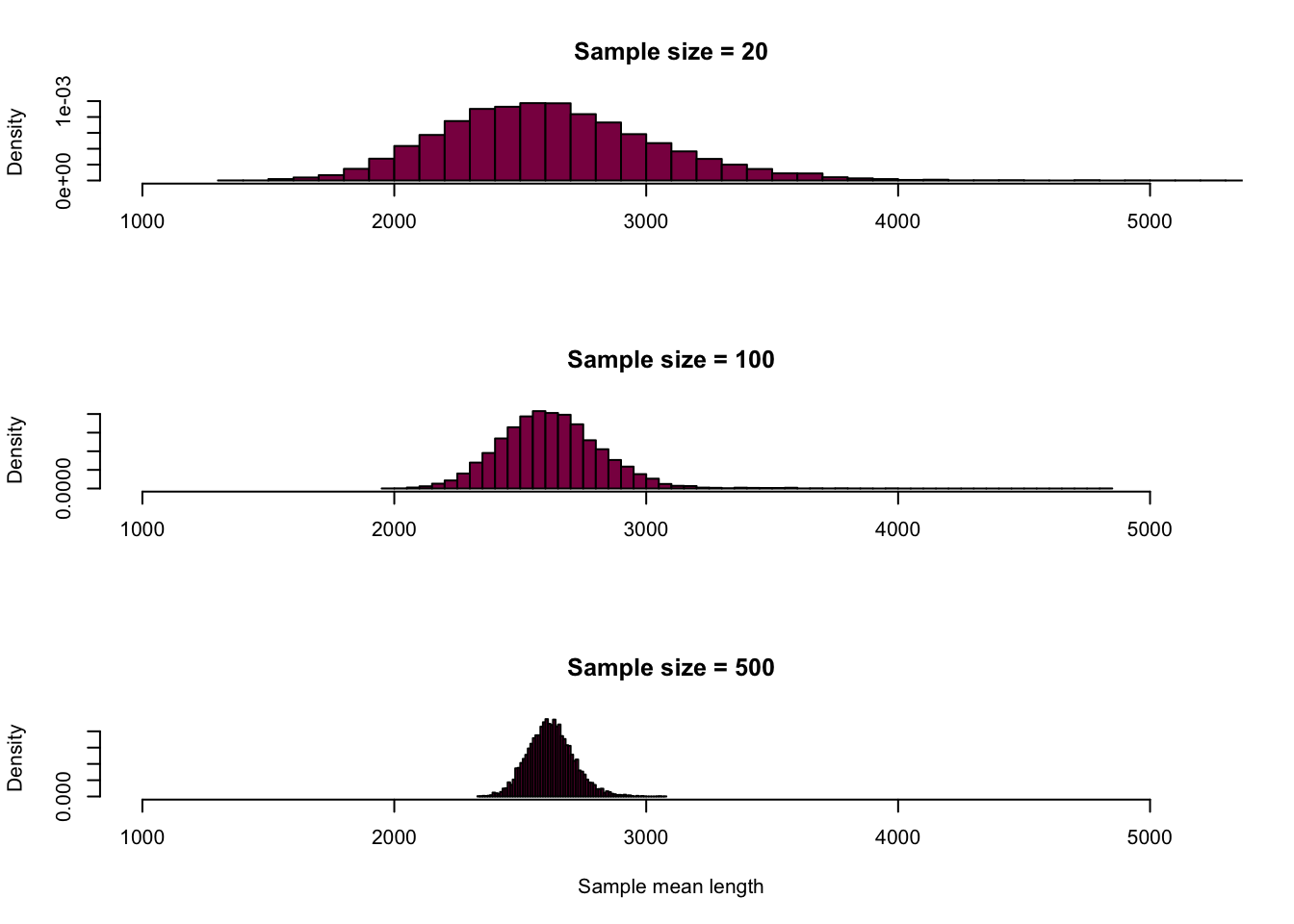

# putting it all together on a "fancier" plot
ggplot() + #creates the canvas 
  geom_histogram(mapping = aes(x = meanLength_20, y=..density..), fill = "red", alpha = 0.6, binwidth = 50, col = "black") + #adds the first histogram 
  geom_histogram(mapping = aes(meanLength_100, y=..density..), fill = "green", alpha = 0.6, binwidth = 50, col = "black") + # adds the second histogram on top of the first
  geom_histogram(mapping = aes(meanLength_500, y=..density..), fill = "deeppink4", alpha = 0.6, binwidth = 50, col = "black") + # adds the third histogram on top
  xlab("Sample mean length")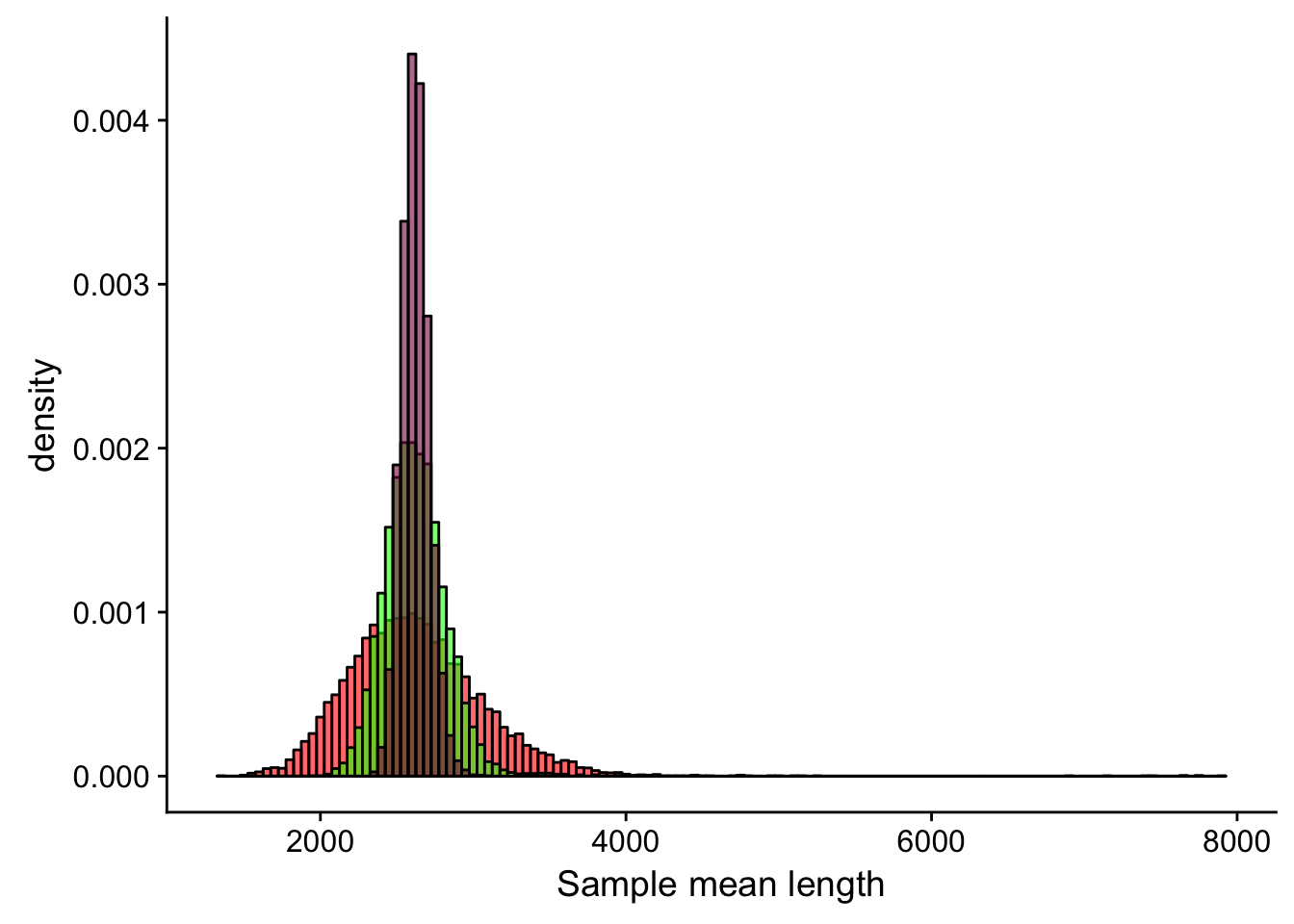

Derive the sampling distribution for the SD in the sample and the median.

Standard deviation:

# this is the exact same code, I'm just calculating the standard deviation instead of the mean

sdLength_100 = NULL
sdLength_20 = NULL
sdLength_500 = NULL

for (i in 1:10000) {
  sample_100_sd = sample(x = HumanGeneLengths$gene.length, size = 100, replace = T)
  sample_20_sd = sample(x = HumanGeneLengths$gene.length, size = 20, replace = T)
  sample_500_sd = sample(x = HumanGeneLengths$gene.length, size = 500, replace = T)
  sdLength_100[i] = sd(sample_100_sd)
  sdLength_20[i] = sd(sample_20_sd)
  sdLength_500[i] = sd(sample_500_sd)
}

par(mfrow=c(3,1))

hist(sdLength_20,
     breaks = 180,
     col = "deeppink4",
     main = "Sample size = 20",
     xlab = "", 
     freq = F)

hist(sdLength_100,
     breaks = 180,
     col = "deeppink4",
     main = "Sample size = 100",
     xlab = "", 
     freq = F)

hist(sdLength_500,
     breaks = 180,
     col = "deeppink4",
     main = "Sample size = 500",
     xlab = "Sample standard deviation", 
     freq = F)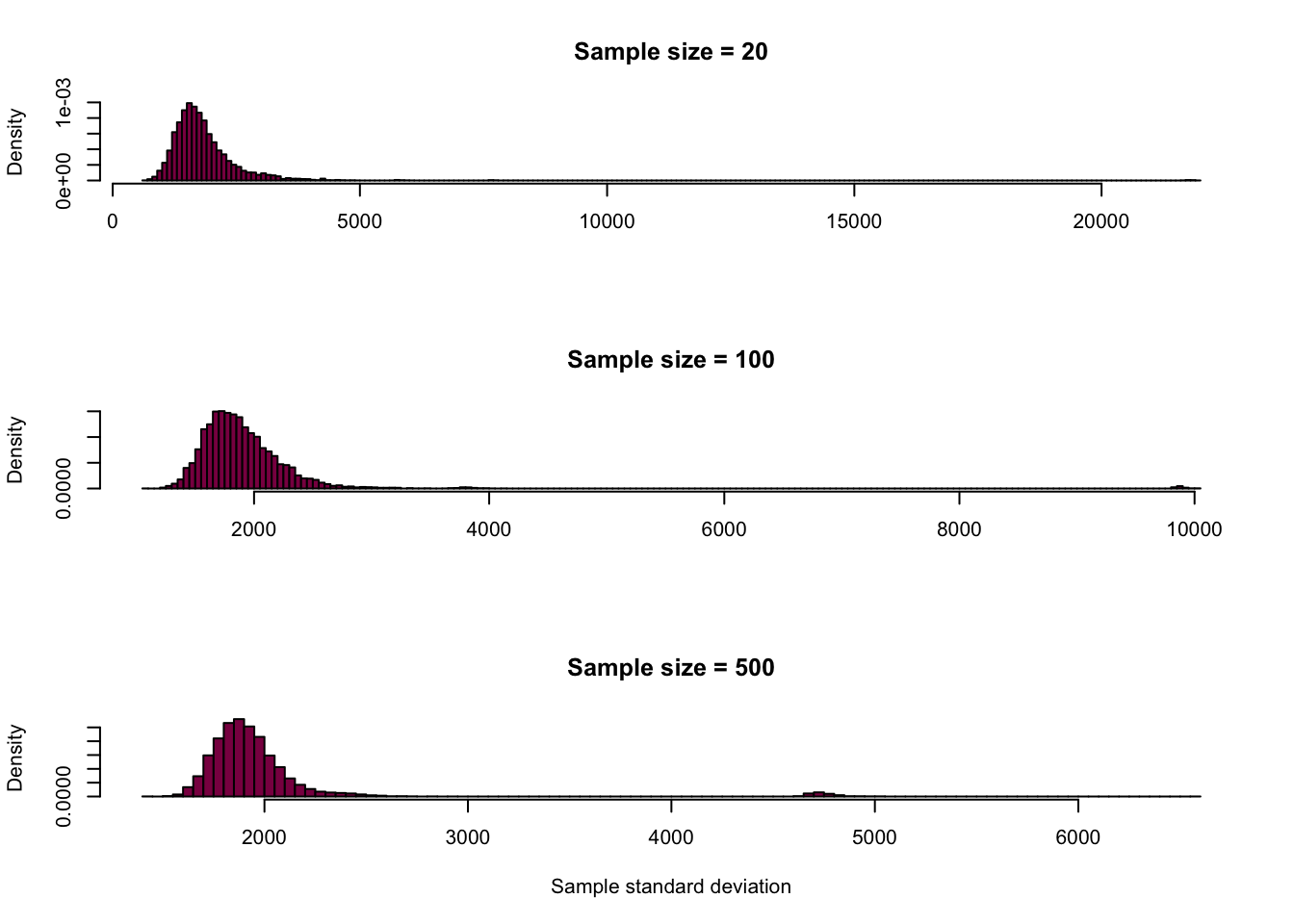

ggplot() +
  geom_histogram(mapping = aes(x = sdLength_20, y=..density..), fill = "red", alpha = 0.6, binwidth = 30) +
  geom_histogram(mapping = aes(sdLength_100, y=..density..), fill = "green", alpha = 0.6, binwidth = 30) +
  geom_histogram(mapping = aes(sdLength_500, y=..density..), fill = "deeppink4", alpha = 0.6, binwidth = 30) +
  xlab("Sample standard deviation")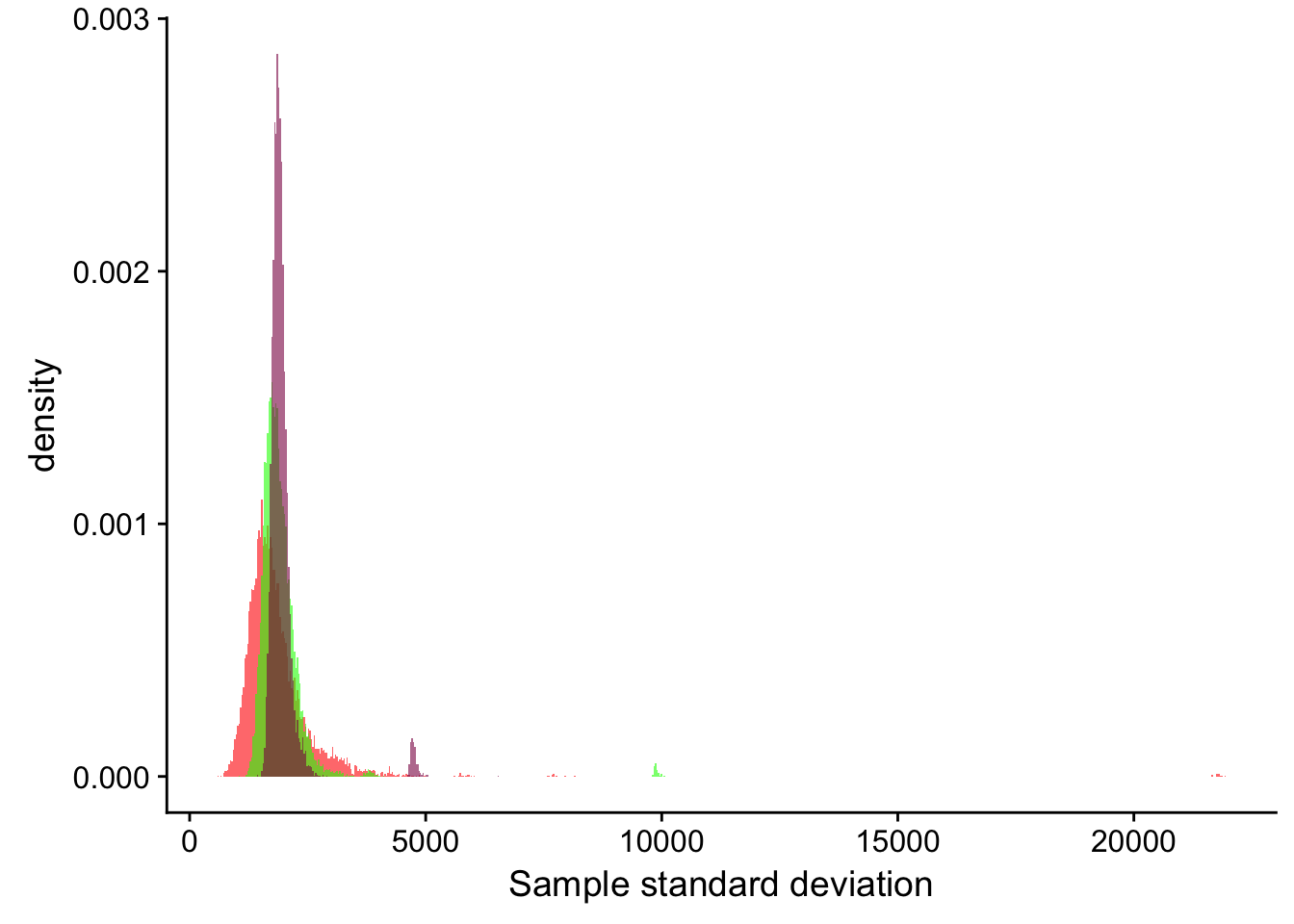

Median:

# also the exact same code, just calculating the median

medianLength_100 = NULL
medianLength_20 = NULL
medianLength_500 = NULL

for (i in 1:10000) {
  sample_100_median = sample(x = HumanGeneLengths$gene.length, size = 100, replace = T)
  sample_20_median = sample(x = HumanGeneLengths$gene.length, size = 20, replace = T)
  sample_500_median = sample(x = HumanGeneLengths$gene.length, size = 500, replace = T)
  medianLength_100[i] = median(sample_100_median)
  medianLength_20[i] = median(sample_20_median)
  medianLength_500[i] = median(sample_500_median)
}

par(mfrow=c(3,1))

hist(medianLength_20,
     breaks = 180,
     col = "deeppink4",
     main = "Sample size = 20",
     xlab = "", 
     freq = F)

hist(medianLength_100,
     breaks = 180,
     col = "deeppink4",
     main = "Sample size = 100",
     xlab = "", 
     freq = F)

hist(medianLength_500,
     breaks = 180,
     col = "deeppink4",
     main = "Sample size = 500",
     xlab = "Sample median", 
     freq = F)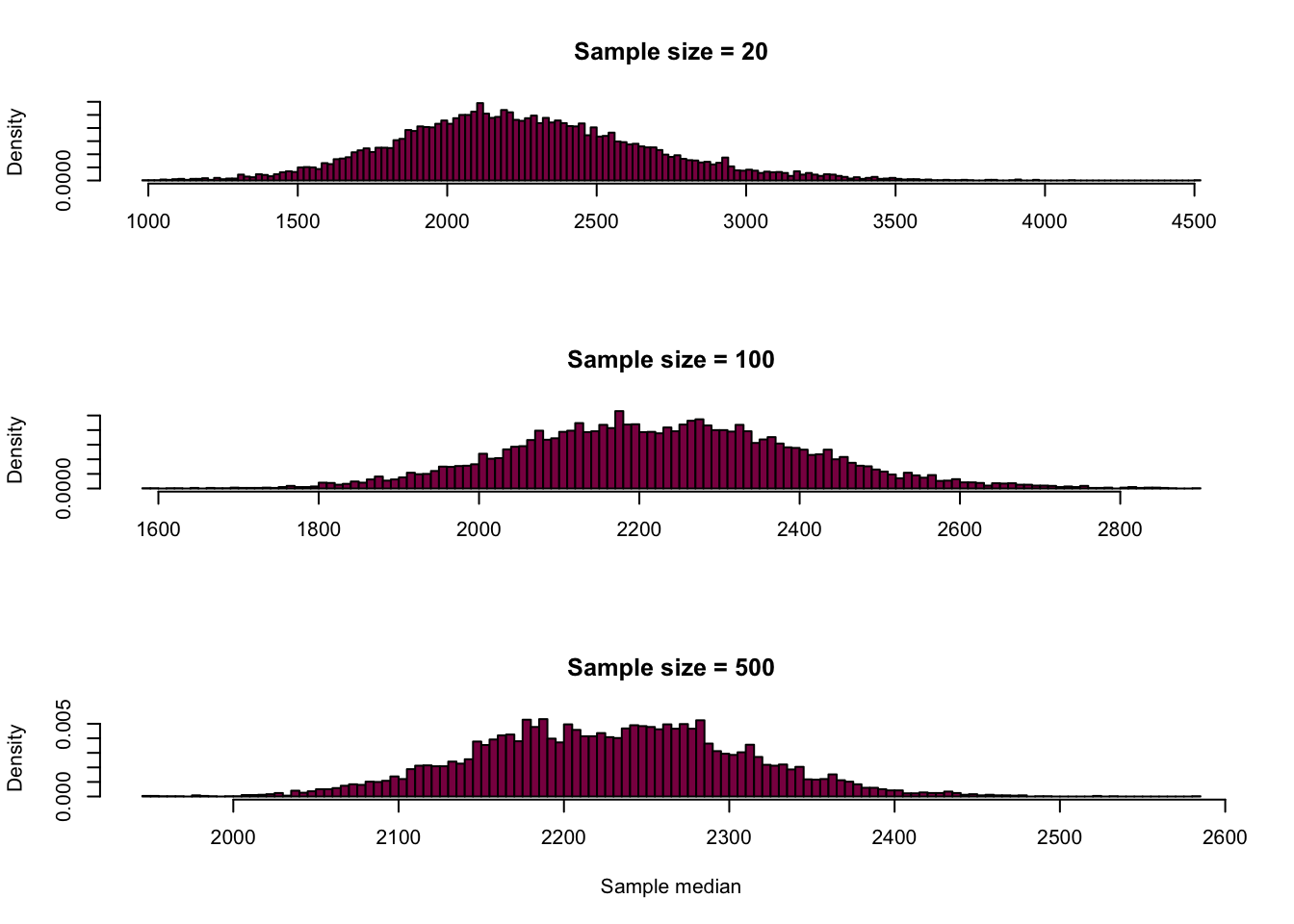

ggplot() +
  geom_histogram(mapping = aes(x = medianLength_20, y=..density..), fill = "red", alpha = 0.6, binwidth = 20, col = "black") +
  geom_histogram(mapping = aes(medianLength_100, y=..density..), fill = "green", alpha = 0.6, binwidth = 20, col = "black") +
  geom_histogram(mapping = aes(medianLength_500, y=..density..), fill = "deeppink4", alpha = 0.6, binwidth = 20, col = "black") +
  xlab("Sample median")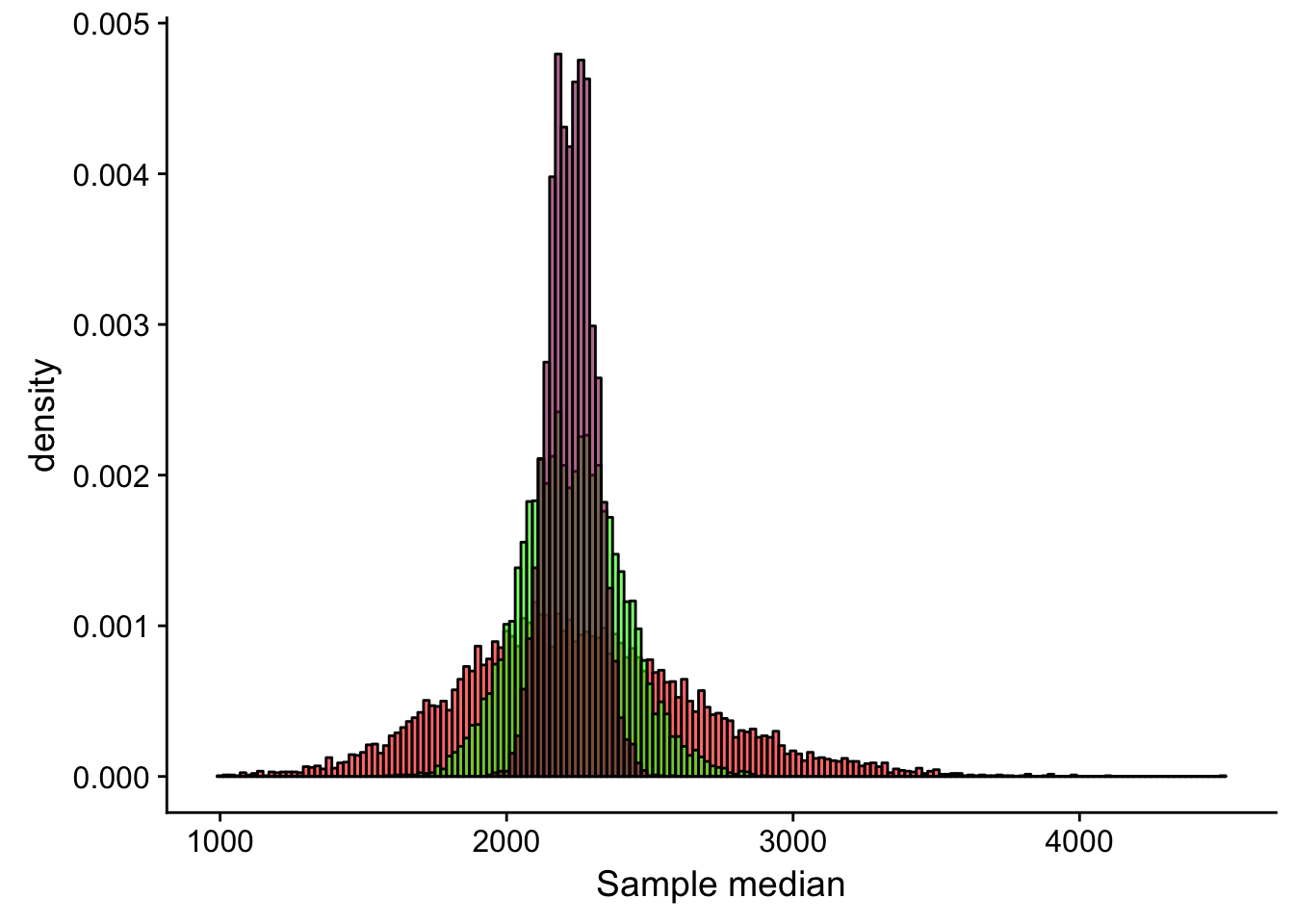

Compare the statistical precision we have to estimate mean SD and median: is the summary statistic that entails most uncertainty?

So we created all these nice sampling distributions and we can calculate the standard error to get an idea about their uncertainty:

sd(meanLength_20)/sqrt(20)

## [1] 100.8671

sd(meanLength_100)/sqrt(100)

## [1] 20.48314

sd(meanLength_500)/sqrt(500)

## [1] 4.057937

sd(sdLength_20)/sqrt(20)

## [1] 216.6111

sd(sdLength_100)/sqrt(100)

## [1] 63.66825

sd(sdLength_500)/sqrt(500)

## [1] 20.30935

sd(medianLength_20)/sqrt(20)

## [1] 93.10885

sd(medianLength_100)/sqrt(100)

## [1] 17.87735

sd(medianLength_500)/sqrt(500)

## [1] 3.5581

We can see that if we compare the precision of our estimates given the 3 sample sizes, the n = 500 estimate is the most precise which is expected. If we take a look at the different summary statistics at the same sample sizes, we find that the median estimate is the least uncertain - this is also expected given that this statistic is the most resistant to the influence of the outliers while the mean and standard deviation are more sensitive to them (remember, the standard deviation is the most uncertain - it is calculated using the mean, which was already pretty sensitive to extreme observations!).

Take me back to the beginning!

4. Trying and evaluating the +/- 2 SEs rule of thumb

Generate 20 samples of n=100 genes from the human gene length distribution, for each sample calculate the mean and CI around the mean using 2SEs

Mean = NULL
SE = NULL
epoch = NULL # don't worry about this, I just needed it for plotting purposes
sample_size = 100

for(i in 1:20){
  sample <- sample(x = HumanGeneLengths$gene.length, size = sample_size,replace = T)
  Mean[i] = mean(sample)
  SE[i] = sd(sample)/sqrt(sample_size)
  epoch[i] = i
}
# putting it all together in a nice dataframe
df <- data.frame() #creating an empty dataframe
df <- data.frame(cbind(epoch, Mean, SE, Mean-2*SE, Mean+2*SE, sample_size)) #binding the columns together
colnames(df) <- c("Sample_nr", "Mean", "Standard_error", "Lower_confidence_limit", "Upper_confidence_limit", "Sample_size") #naming the columns in the dataframe

# a fancy plot to visualize the CIs
ggplot() +
  geom_point(data = df, aes(y = Sample_nr, x = Mean)) +
  geom_segment(data = df, aes(x = Lower_confidence_limit,
                              xend = Upper_confidence_limit, 
                              y = Sample_nr,
                              yend = Sample_nr)) +
  geom_vline(xintercept = mean(HumanGeneLengths$gene.length), col = "deeppink4")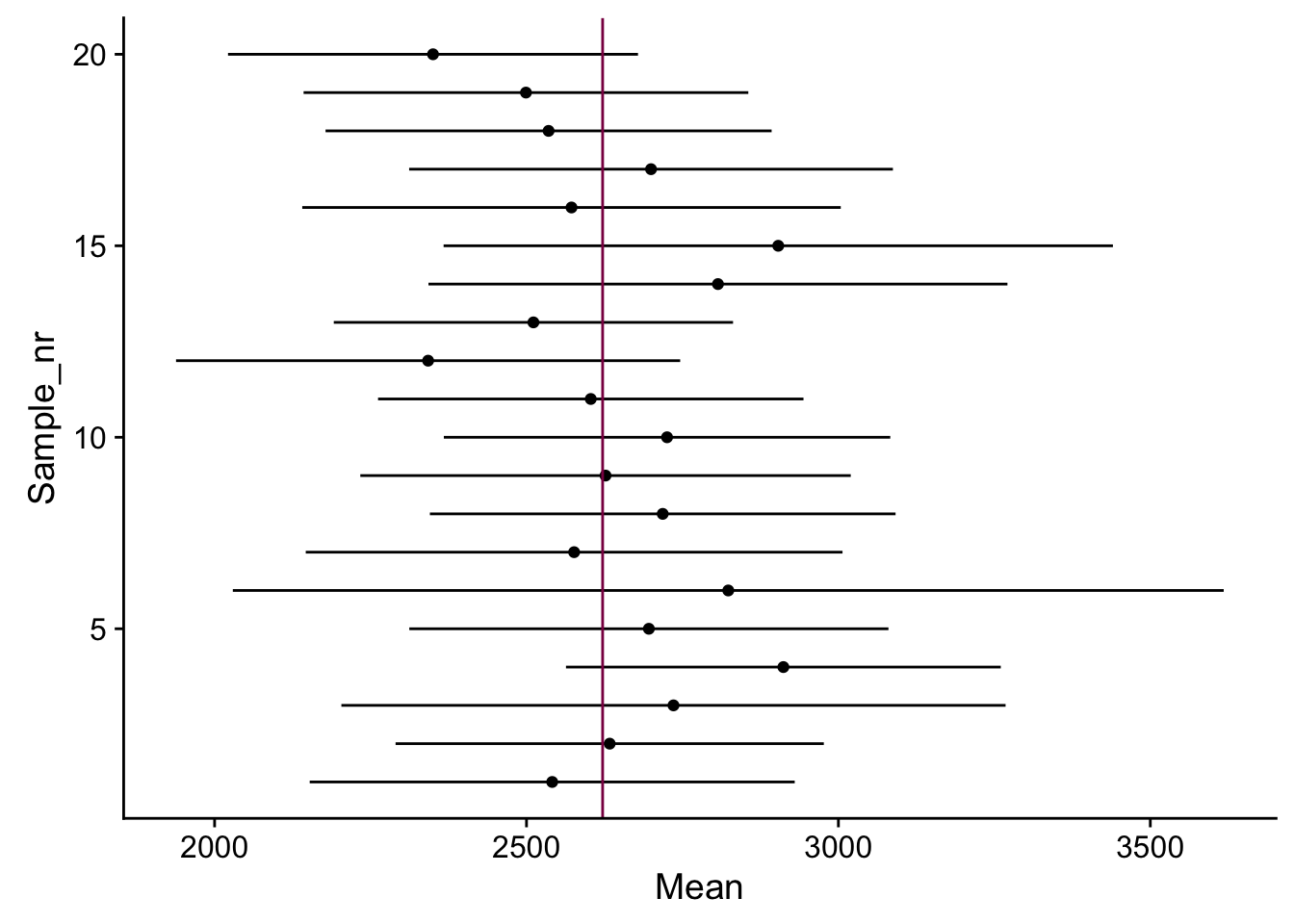

How many intervals out of 20 “cover” the true mean? Is that what we expect for a 95% CI? (if you repeat that several times, numbers vary a bit)

It depends - I ran this code several times and sometimes every interval covered the true mean, sometimes only 17 out of 20, etc. This is not exactly what we would expect from a 95% CI, however, the 2SE rule of thumb is just an approximation and keeping this in mind, it works relatively well.

Just to demonstrate how the CIs change when the sample size gets bigger, let’s increase the sample size…

Mean_1000 = NULL
SE_1000 = NULL
epoch_1000 = NULL
sample_size = 1000


for(i in 1:20){
  sample_1000 <- sample(x = HumanGeneLengths$gene.length, size = sample_size,replace = T)
  Mean_1000[i] = mean(sample_1000)
  SE_1000[i] = sd(sample_1000)/sqrt(1000)
  epoch_1000[i] = 20+i
}
df_1000 <- data.frame(epoch_1000, Mean_1000, SE_1000, Mean_1000-2*SE_1000, Mean_1000+2*SE_1000, sample_size)
colnames(df_1000) <- c("Sample_nr", "Mean", "Standard_error", "Lower_confidence_limit", "Upper_confidence_limit", "Sample_size")
df <- data.frame(rbind(df, df_1000))

Mean_100000 = NULL
SE_100000 = NULL
epoch_100000 = NULL
sample_size = 100000

for(i in 1:20){
  sample_100000 <- sample(x = HumanGeneLengths$gene.length, size = sample_size,replace = T)
  Mean_100000[i] = mean(sample_100000)
  SE_100000[i] = sd(sample_100000)/sqrt(100000)
  epoch_100000[i] = 40+i
}
df_100000 <- data.frame(epoch_100000, Mean_100000, SE_100000, Mean_100000-2*SE_100000, Mean_100000+2*SE_100000, sample_size)
colnames(df_100000) <- c("Sample_nr", "Mean", "Standard_error", "Lower_confidence_limit", "Upper_confidence_limit", "Sample_size")
df <- data.frame(rbind(df, df_100000))

Putting it all together:

ggplot() +
  geom_point(data = df, aes(y = Sample_nr, x = Mean, color = as.factor(df$Sample_size))) +
  geom_segment(data = df, aes(x = Lower_confidence_limit ,
                              xend = Upper_confidence_limit, 
                              y = Sample_nr,
                              yend = Sample_nr,
                              color = as.factor(df$Sample_size))) +
  geom_vline(xintercept = mean(HumanGeneLengths$gene.length)) + 
  ylab("") +
  scale_color_discrete(name = "Sample Size") +
  theme(
  axis.text.y = element_blank(),
  axis.ticks.y = element_blank(),
  axis.line.y = element_blank())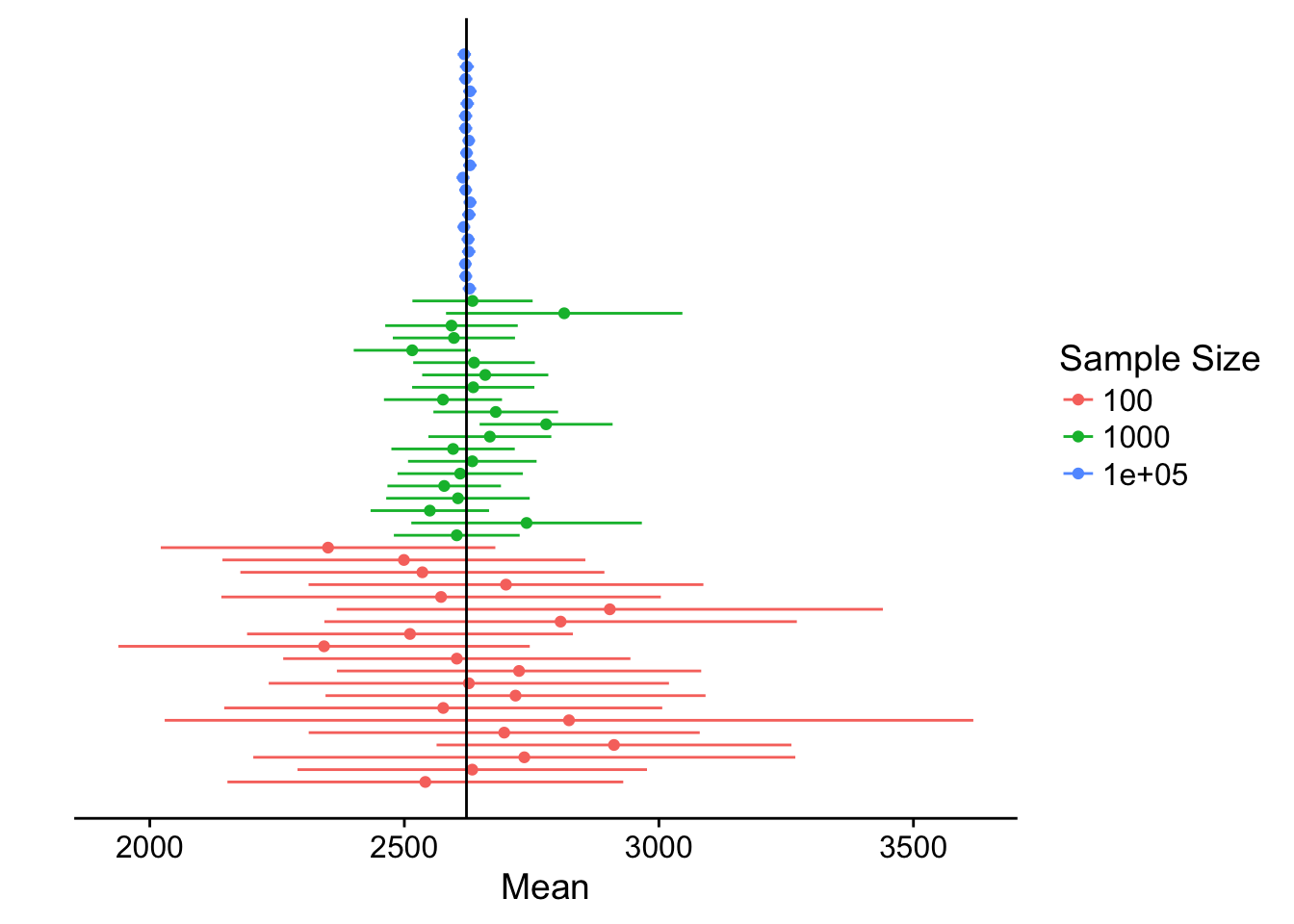

We can see that the bigger the sample size, the narrower the confidence interval - hence, we have more certainty in our estimate.

Take me back to the beginning!

Genome Analysis & Statistics

Week 3: Sampling distributions

Table of contents

Loading libraries

Chapter 4, Problem 9

What type of graph should be used to display these data?

What is the estimated mean number of genes regulated by a regulatory gene in the yeast genome?

What is the standard error of the mean?

Explain what this standard error measures and what assumptions are we making when calculating it.

Exercises

1. Reproducing the Figure 4.1-1 & important details of histogram drawing in R

Take a quick peek at the data and try to find the size of the titin gene (hint: footnote on page 97)

How many genes are in the dataset?

Draw a histogram:

Identify what the options col, main and xlab are allowing you to do.

Why is this graph a BAD display of the data?

Are there 50 bins on the following graph? If not, why not?

Why does R choke here?

What are we doing here?

Look at the Y axis: is this the same Y axis as the book?

What is the difference between frequency of a class and counts of observation per class?

2. Generating Figure 4.1-2

Use the R function sample() to get a vector of 100 observations drawn from HumanGeneLengths and reproduce fig 4.1-2

Discuss what is the conceptual difference between replace = T and replace = F (what should we use here?)

3. Reproducing Figures 4.1-3 and 4.1-4

Adapt this code to generate fig 4.1-3 and 4.1-4 (use 10^4 samples to get the sampling distributions).

Derive the sampling distribution for the SD in the sample and the median.

Compare the statistical precision we have to estimate mean SD and median: is the summary statistic that entails most uncertainty?

4. Trying and evaluating the +/- 2 SEs rule of thumb

Generate 20 samples of n=100 genes from the human gene length distribution, for each sample calculate the mean and CI around the mean using 2SEs

How many intervals out of 20 “cover” the true mean? Is that what we expect for a 95% CI? (if you repeat that several times, numbers vary a bit)